Iteration vs Recursion

One of my goals is to write Haskell at a decent pace, but am still much more fluent at Python. I wanted to translate an algorithm that I wrote awhile back in an iPython Notebook, of traversing in an outward spiral in Python.

Starting at (0,0), the moves increment in a pattern like so:
1 up, 1 right
2 down, 2 left
3 up, 3 right
4 down, 4 left
...

I drew a pretty diagram to show how it looks like graphically.

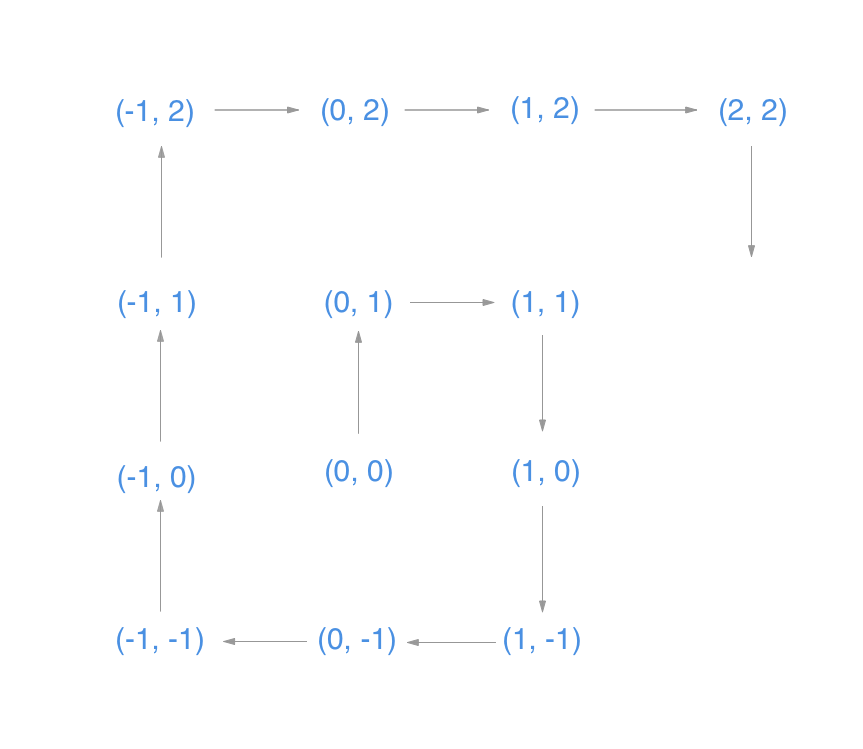
In order to track both the direction and number of steps in that direction, I used two loops. One for the number of steps taken, and one for number of steps taken in a direction. I also created a couple of utility functions (see below) that handle the repetitive steps such as move(coordinates, direction) and change(direction). The additional goals in writing the solution is to make it more readable and easier to maintain, and splitting out these functions makes the spiral function eaiser to digest. Here’s how my solution looks with while loops:

def spiral(n, x=0, y=0, direction=["up", "right", "down", "left"]):
    ind = s = steps_taken = 0
    step_level = 1

    while steps_taken < n:
        # keep moving in direction until step level reached
        while s < step_level:
           (x, y) = move((x, y), direction[ind])
           steps_taken += 1
           s += 1

           if steps_taken == n: return (x, y)

        # reset step counter, if right/left add incr step level
        s = 0
        if ((ind == 1) or (ind == 3)): step_level += 1

        # reaching step level changes direction
        ind = change(ind)

In effort to translate this into Haskell, I basically created similar utility functions. The first utility function is move which takes the direction and current coordinates and returns the next direction. It’s fairly similar in both languages as we’re working with conditionals.

# python
def move((x, y), direction):
    if direction == "up": y += 1
    if direction == "down": y -= 1
    if direction == "right": x += 1
    if direction == "left": x -= 1
    return (x, y)

-- haskell
data Direction = Up | Right' | Left' | Down

move (x, y) direction = case direction of
     Up -> (x, y+1)
     Down -> (x, y-1)
     Right' -> (x+1, y)
     Left' -> (x-1, y)

Next, I have a function that decides on the direction and this is also conditional so it looks imilar. I am using the list structure in Python, whereas I’m using the data type in Haskell.

# this function decides on direction, where
# direction=["up", "right", "down", "left"]
def change(index):
    if index > 2: return 0
    else: return index+1

turn d = case d of
  Up -> Right'
  Down -> Left'
  Right' -> Down
  Left' -> Up

With these utility functions I can go ahead and think about how to keep track of the steps taken. What I want to do with the (x,y) coordinates is figure out when to turn, thus will have to track the goals for the step. So far I have this much written out, for recursively taking steps until the specified number n. I still need to track the step goal for the level so that directions can be specified.

step (x, y) n taken
    | taken <= n = step (x, y) n (taken + 1)
    | otherwise = return (x,y)

Anyway, that’s how far I got this week and will continue to plug away at this and try to finish the solution soon.